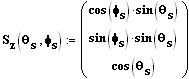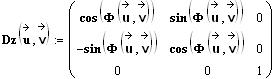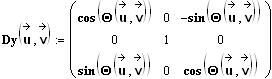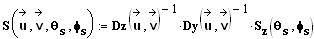Diskret formulierte Standardphysik

Erzeugung von Dunkler Materie und Energie (.pdf des ersten Ansatzes)

Diskret formulierte Standardphysik

23. Anhang:

A1 Definitionen

d Durchmesser der stoßenden Uratome

L (durchschnittliche) freie Weglänge bis zum nächsten Stoß mit 0<L<∞

n Anzahldichte = Teilchenzahldichte (Teilchenzahl N / Volumen V) mit 0<n<1 wegen d > 0

Geschwindigkeit des im Ursprung startenden Teilchens

Geschwindigkeit des Stoßpartners

Relativgeschwindigkeit -   

β Winkel zwischen - und , also Flugwinkel bzw. Bahnenwinkel

ф Herkunftswinkel der Relativgeschwindigkeit = Kollisionswinkel

Θ Drehwinkel der Relativgeschwindigkeit bzw. des Flugwinkels um ,

verschwindet bei sinnvoller Drehung der z-Achse in Ebene mit 

φ Stoßachsenwinkel (Winkel der Berührpunktnormale) erzeugt bzgl. der

Relativgeschwindigkeit, auch Streifwinkel genannt, mit -∏/2<φ<∏/2

θ Drehwinkel der Stoßachse orthogonal um Relativgeschwindigkeit

t Parameter der kontinuierlichen Zeit.

A2 Ausführliche Stoßtransformationen

Für die Untersuchung einer größeren Menge Stöße in einem Gas harter Kugeln eignet sich die Einführung einer sehr einfachen und vor allem leicht zu begründenden Wechselwirkung. Bei der Berührung zweier harter Kugeln kann die Geschwindigkeit wegen des Widerstandes der anderen Kugel in Richtung der Berührpunktnormale nicht weiter mit der ursprünglichen Kugel fortgesetzt werden. Das geht nur auf der anderen Kugel. So überträgt sich der Geschwindigkeitsbetrag parallel zu dieser vollständig auf die jeweils andere Kugel. Orthogonale Geschwindigkeitskomponenten werden dagegen nicht in ihrer freien Bewegung durch den leeren Raum gehindert und setzen sich auf den ursprünglichen Kugeln fort. Die stoßenden Kugeln (Vektoren) und haben jeweils 3 Komponenten.

Für die Stoßachsenermittlung ist zuerst die Relativgeschwindigkeit erforderlich:

(S1)

Die Richtung der Relativgeschwindigkeit wird mit einer Kugelkoordinaten-Transformation ermittelt:

(S2)

(S3)

Diese Funktionen entsprechen den ausführlichen Transformationen gemäß dem Artikel über Kugelkoordinaten in Wikipedia. Dabei gilt 0<Φ<2∏ und 0<Ө<∏.

Stoßachsenwinkel ergeben sich in den Simulationen zufallsabhängig, hängen aber eigentlich deterministisch von der unbekannten Umgebung ab. Der Winkel kann Werte bis annehmen und Werte von 0 bis , wobei gleich wahrscheinliche parallele Bahnen zur Richtung der Relativgeschwindigkeit angenommen werden. Das ist auf gleich wahrscheinliche parallele Bahnen bei den Stoßpartnern zurückzuführen. Damit ergibt sich in kartesischen Koordinaten der Stoßachsenvektor:

Dieser wurde relativ zur Richtung der Relativgeschwindigkeit erzeugt und muss nun im ursprünglichen Koordinatensystem (dem Laborsystem von und ) ausgedrückt werden, was durch zwei hintereinander ausgeführte Drehungen erreicht wird:

Damit ergibt sich die Stoßachse im ursprünglichen Koordinatensystem durch das zweifache Zurückdrehen zu:

Dieses S entspricht beim Zentralstoß auf eine ruhende Kugel dem ursprünglichen bzw. beim Zentralstoß auf ein beliebiges allgemeiner dem Relativgeschwindigkeitsvektor normiert auf 1. Beim Stoß werden nun die zur Stoßachse parallelen Geschwindigkeiten (_p) der beiden beteiligten Kugeln ausgetauscht. Alle Vektoren sollen jedoch weiterhin im ursprünglichen Koordinatensystem betrachtet werden. Die parallelen Komponenten sind:

und die dazu orthogonalen Geschwindigkeitskomponenten (_o):

und somit ergeben sich die Geschwindigkeiten nach dem Stoß:

(S12) und (S13) sind die Stoßtransformationen für dreidimensionale Geschwindigkeitsvektoren. Es sind jeweils Funktionen von acht Parametern, also je drei Geschwindigkeitskomponenten in kartesischen Koordinaten und zwei Winkeln für die sich zufällig ergebende Stoßachse. Diese hier ausführlich abgeleiteten Funktionen hängen jeweils von vorher definierten ab, die alle ineinander eingesetzte dreidimensionale Geschwindigkeitsvektoren sind. Trajektorien (Bahngleichungen), also die Lösungen der Bewegungsgleichungen der bewegten Objekte, ergeben sich daraus durch Multiplikation mit der Zeit. Aus jedem dreidimensionalen Vektor lässt sich jeder andere durch einen geeigneten Stoß erzeugen.

Die Stoßtransformationen enthalten acht Parameter (zwei mal drei für die Geschwindigkeiten und zwei für die Stoßachsenwinkel), welche in Abbildung 3 als Stoßgebilde veranschaulicht sind. Dabei wird nicht die normale Darstellung von Vektoren verwendet, sondern Pfeile, welche gleichzeitig auch den Anfangs- und Endort in einem sinnvoll gewählten Zeitintervall darstellen. Über die mathematischen Eigenschaften eines Gebildes aus den acht bzw. zehn (mit freien Weglängen) reellen Parametern kann und soll hier nicht spekuliert werden. Aber zur Definition der nullten Kraft können diese dienen.

index